EQUAÇÃO DO 2° GRAU
A fórmula quadrática de Sridhara (Bhaskara)
Mostraremos na sequência como o matemático Sridhara, obteve a Fórmula (conhecida como sendo) de Bhaskara, que é a fórmula geral para a resolução de equações do segundo grau. Um fato curioso é que a Fórmula de Bhaskara não foi descoberta por ele mas pelo matemático hindu Sridhara, pelo menos um século antes da publicação de Bhaskara, fato reconhecido pelo próprio Bhaskara, embora o material construído pelo pioneiro não tenha chegado até nós.
O fundamento usado para obter esta fórmula foi buscar uma forma de reduzir a equação do segundo grau a uma do primeiro grau, através da extração de raízes quadradas de ambos os membros da mesma.
DEFINIÇÃO
Uma equação do 2º grau com uma variável tem a forma:
ax² + bx + c = 0
onde os números reais a, b e c são os coeficientes da equação, sendo que a deve ser diferente de zero. Essa equação é também chamada de equação quadrática, pois o termo de maior grau está elevado ao quadrado
x é a incógnita
a,b, e c números reais, chamados de coeficientes
Equação Completa do segundo grau
Uma equação do segundo grau é completa, se todos os coeficientes a, b e c são diferentes de zero.
Exemplos:
1) 2 x² + 7x + 5 = 0, onde a = 2, b = 7 e c = 5
2) 3 x² + x + 2 = 0, onde a = 3 , b = 1 e c = 2
3) x² -7 x + 10 = 0, onde a = 1, b = -7 e c = 10
4) 5x² - x -3 = 0, onde a = 5, b = -1 e c = -3
Resolução de equações completas do 2° grau
Como vimos, uma equação do tipo: ax² + bx + c= 0, é uma equação completa do segundo grau e para resolvê-la basta usar a fórmula quadrática (atribuída a Bhaskara), que pode ser escrita na forma:
Δ = b²- 4ac é o discriminante da equação.
Para esse discriminante Δ, há três possíveis situações:
1) Δ > 0 , a equação te duas raízes reais e diferentes.
2) Δ = 0, a equação tem uma raiz
3) Δ < 0 , a equação não tem raízes reais
Mostraremos agora como usar a fórmula de Bhaskara para resolver a equação:
x² - 5 x + 6 = 0
1) Identificar os coeficientes: a = 1, b = -5, c = 6
2) Escrever o discriminante Δ = b²-4ac.
3) Calcular Δ = (-5)² -4×1×6 = 25-24 = 1
4) Escrever a fórmula de Bhaskara:
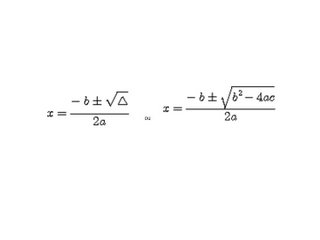
EXEMPLOS

EXERCÍCIOS
1. Calcular o discriminante de cada equação e analisar as raízes em cada caso:
a) x² + 9 x + 8 = 0 (R:-1 e -8)
b) 9 x² - 24 x + 16 = 0 (R:4/3)
c) x² - 2 x + 4 = 0 (vazio)
d) 3 x² - 15 x + 12 = 0 (R: 1 e 4)
e) 10 x² + 72 x - 64 = 0 (R:-8 e 4/5)
e) 5x² - 3x - 2 = 0 (R: 1 e -2/5)
f) x² - 10x + 25 = 0 (R: 5)
g) x² - x - 20 = 0 (R: 5 e -4)
h) x² - 3x -4 = 0 (R: 4 e -1)
i) x² - 8x + 7 = 0 (R: 7 e 1)
RESOLVA AS EQUAÇÕES DE 2º GRAU
1) x² - 5x + 6 = 0 _____(R:2,3)
2) x² - 8x + 12 = 0 ______(R:2,6)
3) x² + 2x - 8 = 0______ (R:2,-4)
4) x² - 5x + 8 = 0 ______(R:vazio)
5) 2x² - 8x + 8 = 0_______ (R:2,)
6) x² - 4x - 5 = 0_______ (R:-1, 5)
7) -x² + x + 12 = 0_______ (R:-3, 4)
8) -x² + 6x - 5 = 0_______ (R:1,5)
9) 6x² + x - 1 = 0______ (R:1/3 , -1/2)
10) 3x² - 7x + 2 = 0 ______(R:2, 1/3)
11) 2x² - 7x = 15 _______(R:5, -3/2)
12) 4x² + 9 = 12x______ (R:3/2)
13) x² = x + 12 ______(R:-3 , 4)
14) 2x² = -12x - 18 _____(R:-3 )
15) x² + 9 = 4x_____ (R: vazio)
16) 25x² = 20x – 4 ____(R: 2/5)
17) 2x = 15 – x² ______(R: 3 , -5)
18) x² + 3x – 6 = -8____ (R:-1 , -2)
19) x² + x – 7 = 5 ____(R: -4 , 3)
20) 4x² - x + 1 = x + 3x² ___(R: 1)
21) 3x² + 5x = -x – 9 + 2x²____ (R: -3)
22) 4 + x ( x - 4) = x _____(R: 1,4)
23) x ( x + 3) – 40 = 0 _____(R: 5, -8)
24) x² + 5x + 6 = 0 _____(R:-2,-3)
25) x² - 7x + 12 = 0 _____(R:3,4)
26) x² + 5x + 4 = 0 _____(R:-1,-4)
27) 7x² + x + 2 = 0 _____(vazio)
28) x² - 18x + 45 = 0 _____(R:3,15)
29) -x² - x + 30 = 0 _____(R:-6,5)
30) x² - 6x + 9 = 0 _____(R:3)
31) ( x + 3)² = 1_______(R:-2,-4)
32) ( x - 5)² = 1_______(R:6,4)
33)( 2x - 4)² = 0_______(R:2)
34) ( x - 3)² = -2x²_______(R:vazio)
35)Na equação 3x² - 12 = 0 as soluções são:
a)0 e 1
b)-1 e 1
c)-2 e 2 (x)
d)-3 e 3
e)0 e 4
36) x² + 3x - 28 = 0 (R: -7,4)
37) 3x² - 4x + 2 = 0 (R: vazio)
38) x² - 3 = 4x + 2 (R: -1,5)
PROBLEMAS COM EQUAÇÃO DO 2° GRAU
1) A soma de um numero com o seu quadrado é 90. Calcule esse numero. (R:9 e-10)
2) A soma do quadrado de um número com o próprio número é 12. Calcule esse numero (R: 3 e -4)
3) O quadrado menos o dobro de um número é igual a -1. Calcule esse número. (R:1)
4) A diferença entre o quadrado e o dobro de um mesmo número é 80. Calcule esse número (R:10 e -8)
5) O quadrado de um número aumentado de 25 é igual a dez vezes esse número. Calcule esse número (R: 5)
6) A soma do quadrado de um número com o seu triplo é igual a 7 vezes esse número. Calcule esse número.(R: 0 e 4)
7) O quadrado menos o quádruplo de um numero é igual a 5. Calcule esse número (R: 5 e -1)
8) O quadrado de um número é igual ao produto desse número por 3, mais 18. Qual é esse numero? (R: 6 e -3)
9) O dobro do quadrado de um número é igual ao produto desse numero por 7 menos 3. Qual é esse numero? (R:3 e ½)
10) O quadrado de um número menos o triplo do seu sucessivo é igual a 15. Qual é esse numero?(R: 6 e -3)
11) Qual o número que somado com seu quadrado resulta em 56? (R:-8 e 7)
12) Um numero ao quadrado mais o dobro desse número é igual a 35. Qual é esse número ? (R:-7 e 5)
13) O quadrado de um número menos o seu triplo é igual a 40. Qual é esse número? (R:8 e -5)
14) Calcule um número inteiro tal que três vezes o quadrado desse número menos o dobro desse número seja igual a 40. (R:4)
15) Calcule um número inteiro e positivo tal que seu quadrado menos o dobro desse número seja igual a 48. (R:8)
16) O triplo de um número menos o quadrado desse número é igual a 2. Qual é esse número? (R:1 e 2)
17) Qual é o número , cujo quadrado mais seu triplo é igual a 40? ( R: 5 , -8)
18) O quadrado de um número diminuido de 15 é igual ao seu dobro. Calcule esse número.
(R: 5 e -3)
19) Determine um número tal que seu quadrado diminuído do seu triplo é igual a 28. (R:7 e -4)
20) Se do quadrado de um número, negativo subtraimos 7, o resto será 42. Qual é esse número?
(R: -7)
21) A diferença entre o dobro do quadrado de um número positivo e o triplo desse número é 77. Calcule o número. (R: 7)
22) Determine dois números ímpares consecutivos cujo produto seja 143. (R: 11 e 13 ou -11, -13)
23) Um azulejista usou 2000 azulejos quadrados e iguais para revestir 45m² de parede. Qual é a medida do lado de cada azulejo? (R:15 cm)
RESOLUÇÃO DE EQUAÇÃO INCOMPLETAS
Resolver uma equação é determinar todas as suas soluções. Vejamos, através de exemplos, como se resolvem as equações incompletas do 2° grau
1° CASO – equações da forma ax² + c = 0, (b = 0)
Exemplos:
1) x² - 25 = 0
x² = 25
x = √25
x = 5
logo V= (+5 e -5)
2) 2x² - 18 = 0
2x² = 18
x² = 18/2
x² = 9
x = √9
x = 3
logo V= (-3 e +3)
3) 7x² - 14 = 0
7x² = 14
x² = 14/7
x² = 2
x = √2
logo V = (-√2 e +√2)
4) x²+ 25 = 0
x² = -25
x = √-25
obs: não existe nenhum número real que elevado ao quadrado seja igual a -25
EXERCÍCIOS
1) Resolva as seguintes equações do 2° grau
a) x² - 49 = 0 (R: -7 e +7)
b) x² = 1 (R: +1 e -1)
c) 2x² - 50 = 0 (R: 5 e -5)
d) 7x² - 7 = 0 (R: 1 e -1)
e) 5x² - 15 = 0 (R: √3 e -√3)
f) 21 = 7x² (R: √3 e -√3)
g) 5x² + 20 = 0 (R: vazio)
h) 7x² + 2 = 30 (R: 2 e -2 )
i) 2x² - 90 = 8 (R: 7 e -7)
j) 4x² - 27 = x² (R:3 e -3)
k) 8x² = 60 – 7x² (R: 2 e -2)
l) 3(x² - 1 ) = 24 (R: 3 e -3)
m) 2(x² - 1) = x² + 7 (R:3 e -3)
n) 5(x² - 1) = 4(x² + 1) (R:3 e -3)
o) (x – 3)(x + 4) + 8 = x (R:2 e -2)
p) 4x²= 36 (R: 3, -3)
q) 4x² - 49 = 0 ( R: 7/2, -7/2)
r) 16 = 9x² (R: 4/3 , -4/3)
s) 3x² + 30 = 0 (R: vazio)
t) 9x² - 5 = 0 (R: √5/3 , -√5/3)
2° CASO: Equações da forma ax² + bx = 0 ( c = 0)
Propriedade: Para que um produto seja nulo é preciso que um dos fatores seja zero .
Exemplos
1) resolver x² - 5x = 0
fatorando x ( x – 5) = 0
deixando um dos fatores nulo temos x = 0
e o outro x – 5 = 0 , passando o 5 para o outro lado do igual temos x = 5
logo V= (0 e 5)
2) resolver: 3x² - 10x = 0
fatorando: x (3x – 10) = 0
deixando um dos fatores nulo temos x = 0
Tendo também 3x – 10 = 0
3x = 10
x = 10/3
logo V= (0 e 10/3)
Observe que, nesse caso, uma das raízes é sempre zero.
EXERCÍCIOS
1) Resolva as seguintes equações do 2° grau.
a) x² - 7x = 0 (R: 0 e 7)
b) x² + 5x = 0 (R: 0 e -5)
c) 4x² - 9x = 0 (R: 0 e 9/4)
d) 3x² + 5x =0 (R: 0 e -5/3)
e) 4x² - 12x = 0 (R: 0 e 3)
f) 5x² + x = 0 (R: 0 e -1/5)
g) x² + x = 0 (R: 0 e -1)
h) 7x² - x = 0 (R: 0 e 1/7)
i) 2x² = 7x (R: 0 e 7/2)
j) 2x² = 8x (R: 0 e 4)
k) 7x² = -14x (R: 0 e -2)
l) -2x² + 10x = 0 (R: 0 e 5)
2) Resolva as seguintes equações do 2° grau
a) x² + x ( x – 6 ) = 0 (R: 0 e 3)
b) x(x + 3) = 5x (R: 0 e 2)
c) x(x – 3) -2 ( x-3) = 6 (R: 0 e 5)
d) ( x + 5)² = 25 (R: 0 e -10)
e) (x – 2)² = 4 – 9x (R: 0 e -5)
f) (x + 1) (x – 3) = -3 (R: 0 e 2)
EQUAÇÃO FRACIONÁRIA DO 2º GRAU
Nessas equações (há incónita no denominador), devemos garantir que nenhum dos denominadores se anule
exemplos:
vejamos através de exemplos, como se resolvem as equações fracionárias.
exemplo 1
exemplo 2
EXERCÍCIOS
1) Resolva as equações do 2º grau em R
EQUAÇÕES LITERAIS
Nessas equações, além da incógnita x , aparecem outras letras (a,b,c,m,n ....), que são chamadas de parâmetros, vamos resolver a equação:
EXERCÍCIOS















50 Comments:
Ótimo esse site só que tinha que ter o desenvolvimento !
bom , eu tó com trabalho de matematica para fazer só que eu não sei e nesse saite tem tudo o que eu presciso só que só tem as resposta ai fica complicado porque se eu pegar só a resposta a professora não vaii quere o trabalho por favor alguém me ajuda ?
bom , eu tó com trabalho de matematica para fazer só que eu não sei e nesse saite tem tudo o que eu presciso só que só tem as resposta ai fica complicado porque se eu pegar só a resposta a professora não vaii quere o trabalho por favor alguém me ajuda ?
achei legall este site ele tras muitas informacoes para oss alunos q nao sabem ...eu nao preciso disso pois sou a segunda maisss inteligente da minha sala entao fiz as contas e cheguei ao resultado certo sem nenhuma dificuldade olha q estou no 7ano da 6serie e tenho 12 anosss
QUAL E O NUMERO CUJO O DOBRO E IGUAL AOS SEUS 3/4 AUMENTADOS DE 15?
om me mostra a resoluçao
da equaçao do 2 grau completa
vlw mesmo pessoal eu tirei 2 no teste e agora vou tirar um 10 o site e otimo ta tudo bem explicado e ensima mesmo muito obrigado mesmo
interessante o site!
Eu adorei o site tenho prova hoje e tirei ass minhas duvidas ainda bem!!! muito bom msm
eu gostaria que tivessem pelo menos umas 5 contas resolvidas para exemplificar melhor !! mas ta tudo blz o site!! :P
Vc poderia explicar como fazer cada questao, que ficaria perfect!
Ja ta nos meus favr.
Adoorei o site, tenho muita dificuldade em matemática e tirei nota baixa, peguei os exercícios para resolver e depois vou ler as explicações. Concerteza, vaai me ajudar ! Já tá nos meus favoritos.
Thais e mais alguém que quizer trabalho de matemática com resolução me adiciona no msn: and.joy@hotmail.com aah e adorei o site, me ajudo bastante pra estudar
Nossa que legal, esse site muito explicativo, gostei de verdadee me ajudou bastante em algumas atividades.Eu até peguei alguns problemas de equação do 2 graupara resolver. Me ajudou bastante. Parabéns pelo seu site. Visita o meu blog é http//fernandogesto.blogspot.com
olha achei maravilhoso, mas não consigo aprender,minha cabeça doi de tanto tentar já estou pensado em desistir pois não entra nada na minha cabeça muito obrigada.
eu gostei mto da explicação, dos exercícios e tal ,mas acho que tinha que ter o desenvolvimento . Pra mim só faltou isso .
como efetua esta conta9(21 x):(3 x)?,para 3x
Ótimo post ta me ajudando bastante ;)
Poxa. Tudo muito completo. Valeu aí.
muito bom !!!
vlw aí.
É eu estava fazendo um programa para executar Equações do Segundo Grau e peguei algumas das equações que você deu como exercícios, e uma delas a resposta está errada:
É a Equação 9 x² - 24 x + 16 = 0
de uma olhada, e caso queria a resposta me comunique haha
gatun_10@hotmail.com
eu gostei deste site mas tem um pequeno probleminha que falta mais exemplos de como se resolve as tais equaçoes.
nossa cara,eu até que gostei,mas não tem as equações que eu quero!!!
como faço ? 49 x ² +9 = 0
so falta a resposta
nathalia
olá povão
Thais
obriga pela ajuda!!!
parabens pelo site
bom esse site , podia ter videos de prof , ou alunos msmo , mostrando o desennvolvimento das contas !
add msn nay.carcheno@hotmail.com ensino qualquer coisa sobre matematica!
sou fera em matematica me add em nay.carcheno@hotmail.com
quanto que dá a soma de um número positivo com o seu quadrado é igual a 132
x = 11
ADOREIIIIIIIII ESSE BLOGGER
TUDO QUE EU QERIA EU ACHEI É MUITO BOM MESMO ESPLICA TUDINHO , QERO QUE TENHA MAIS E MAIS DESENVOLVIMENTO E EU SEMPRE ESTEREI PASSANDO PORAQUE
ADOREII ESSE BLOGGER ESPERO QUE TENHA MAIS COISAS PORAQI ADOREI
Nossa , assim como eu olhei o You tube aquiii também é ótimo .
Parabéns
Ok pessoal como posso resolver este problema: numa cidade a população no ano 2000 era de 1784000, no ano de 2007 a população passou a ser de 1939000, no ano 2010 tivemos uma população de 2068000. A pergunta é Qual será a população desta mesma cidade no ano 2020. como armar e desenvolver este proplema.
ruc-10@hotmail.com
Kra a questao 29 a Resposta é -5 e 4 isso do exercicio de equaçao do 2 grau lá em cima abraço!
This comment has been removed by the author.
Boa noite,
Eu estava fazendo o exercicio B, porém o meu resultado não esta igual, meu delta deu 0, e minha solução deu 3, ACHO que esta errado !! Obrigado pela atenção !
Muito bom!
Agora eu deixo uma sugestão: este site resolve equações do segundo grau e ainda exibe seu gráfico!
http://calculadoraonline.com.br/equacao-2-grau
Muito bom, mas eu deixo uma sugestão de calculadora que resolve equações e ainda mostra gráfico delas:
http://calculadoraonline.com.br/equacao-2-grau
eu fiz uma atividade que tinha uma conta que era assim: x²=x+12=0 , e eu nao consegui fazer e acho que vou ficar sem fazer , ajuda?
eu fiz uma atividade que tinha uma conta que era assim: x²=x+12=0 , e eu nao consegui fazer e acho que vou ficar sem fazer , ajuda?
8) O quadrado de um número é igual ao produto desse número por 3, mais 18. Qual é esse numero? (R: 6 e -3)
passa ?
Muito obrigado, ajudou muito os seus exercícios(principalmente por ter as respostas)!!!
Valeu...
Gostei das informações. Está tudo muito bem explicado com todos os detalhes.
gente vamos prestar atenção no sinal
Vc podia mostra passo a passo ne
Queria ver o passo a passo
bom dia, gostei muito das questões gostaria de saber como desenvolver a questão 23, do exercicio, problemas com equação do 2º GRAU acima. um azuleijista usou 2000 azuleijos quadrados e iguais para revestir 45m quadrados de parede. qual é a medida do lado de cada azulejo?
Post a Comment
<< Home